Acoustic Signature of a Tea Kettle
In an adiabatic environment like the atmosphere on the earth's surface, sound propagates through the medium of air and produces a phenomenon called acoustic resonance. Resonance describes the tendency of a system to amplify sound waves at a wavelength proportional to a characteristic dimension of the environment. This means that the natural frequencies of a room are proportional to the dimensions of the room (assuming simple geometries, of course), and the modes of a vibrating string are proportional to its length. This mechanism is the foundation for musical instruments, seismic behavior of the earth, the human vocal tract, and many other applications involving wave phenomena [see more here and here]. For the experiment here, I will explore the acoustic signature of a tea kettle and a few hypotheses as to the observations.
Acoustics and Standing Wave Phenomena
Any discussion of acoustics must begin with a review of sinusoidal oscillations and wave propagation. Acoustics waves can best be characterized as a longitudinal disturbance in a medium. In air, we use adiabatic approximations to simplify the fundamental equations of fluid dynamics. Evidently, the wave equation will be employed and solutions in the form of sinusoids. The wave equation for acoustics is often stated as:
where p represents a pressure disturbance, c is the speed of sound in the medium, and t is time. The wave equation has a 3-dimensional solution of the form:
where values for k are a function of the frequency and speed of sound. For a simplified form of the current problem, I will assume a 1-D wave equation and solution. Therefore, in the case of a pipe or channel, the solution reduces to the following:
Depiction of standing wave phenomena in closed-ended channels.
Solutions to the above boundary conditions follow:
And finally, the ubiquitous standing wave frequency can be recovered as follows:
Helmholtz Resonators
A Helmholtz resonator is a device that consists of a cavity and a neck that behave like a mass-spring system with a resistance element, capacitive element, and inductive element. The resonator is a simplified acoustic system where one can obtain the resonance frequency by knowing the dimensions of the device. I won't cover all the details here because the general mathematics is quite extensive, however, the equation for predicting the resonance is as follows:
Helmholtz resonator showing the primary components that contribute to the resonance: cavity volume, neck length, and neck cross-sectional area.
Now, I'm sure some may be wondering what all of this background has to do with the experiment involving a tea kettle - and I understand that. However, the basics of acoustics, standing waves, and even resonance was important to truly break down the behavior of such a complex system. A steam whistle (tea kettle) may seem like a very simple mechanism. It is simple for humans to produce whistles and they are ubiquitous in train systems, nonetheless, they are quite nonlinear, difficult, and complex feats of engineering. Just recently a research group in Cambridge extensively researched and modeled the tea kettle and its mechanisms that produce sound. And for a truly in-depth analysis and investigation of the tea kettle I recommend their paper (here), however, it's too complex for a blog like this. Decidedly, I chose to cover the basics of standing waves and Helmholtz resonators as a simplified introduction to the acoustic behavior of a steam kettle to use a more simplified model of dimensional analysis to investigate the acoustic emissions of a steam kettle.
Application of Helmholtz Resonance and Standing Waves to a Tea Kettle
The steam kettle used is shown on the right. It is a standard stovetop tea kettle that has a water capacity of 8 cups, a neck length of roughly 2", a neck diameter of about 1.125", and a whistle hole diameter of roughly 0.25". The part of the kettle that is responsible for the high-pitch sonic phenomenon is what is called the whistle. The dimensions of the whistle are (very roughly):
The research team from Cambridge (see above) indicate that there are two modes to a steam whistle: i. the Helmholtz resonance phase and ii. the vortex shedding phase that radiates sound at the frequency of the upstream neck of the kettle. For the Helmholtz phase (using the equation above) I found a resonance frequency range between 1400Hz and 2500Hz. This range is a result of effective length approximations and the corrections for speed of sound at various temperatures in steam and air. The Helmholtz resonance equation was found to be in the following form:
Tea kettle neck profile - the upstream neck is the proposed mechanism for the standing wave frequency found for high reynolds numbers.
Next, I attempted to find the second phase of the kettle whistle: the point where it approaches a pseudo-steady state. This was suggested again by the Cambridge researchers. The approach is simple: assume the constant whistle of the kettle is caused by radiation from a jet produced by the turbulent ejection from the upstream neck through the whistle and out of the end of the whistle hole. The suggestion intimates that the sound that is heard at the final stage of the boiling water in the kettle is due to the standing waves setup in the neck of the kettle being radiated out from the whistle - which is contrary to the belief that the first stage of the kettle noise is due to a Helmholtz resonance.
This assumption of standing waves produced by the neck geometry is carried out by utilizing the standing wave equation derived earlier for a half-open, half-closed pipe:
For the tea kettle, the length is assumed to be the length of the yellow neck shown above in the photo. The speed of sound is again variable, as we don't know the exact temperature or pressure within the kettle. The fundamental frequency of the system during its steady state should therefore fall between 1700Hz and 2500Hz. And now that the calculations are finished, I will focus on the experimental verification and results from collecting data from several steam whistle measurements.
Investigating A Tea Kettle and its Acoustic Signature
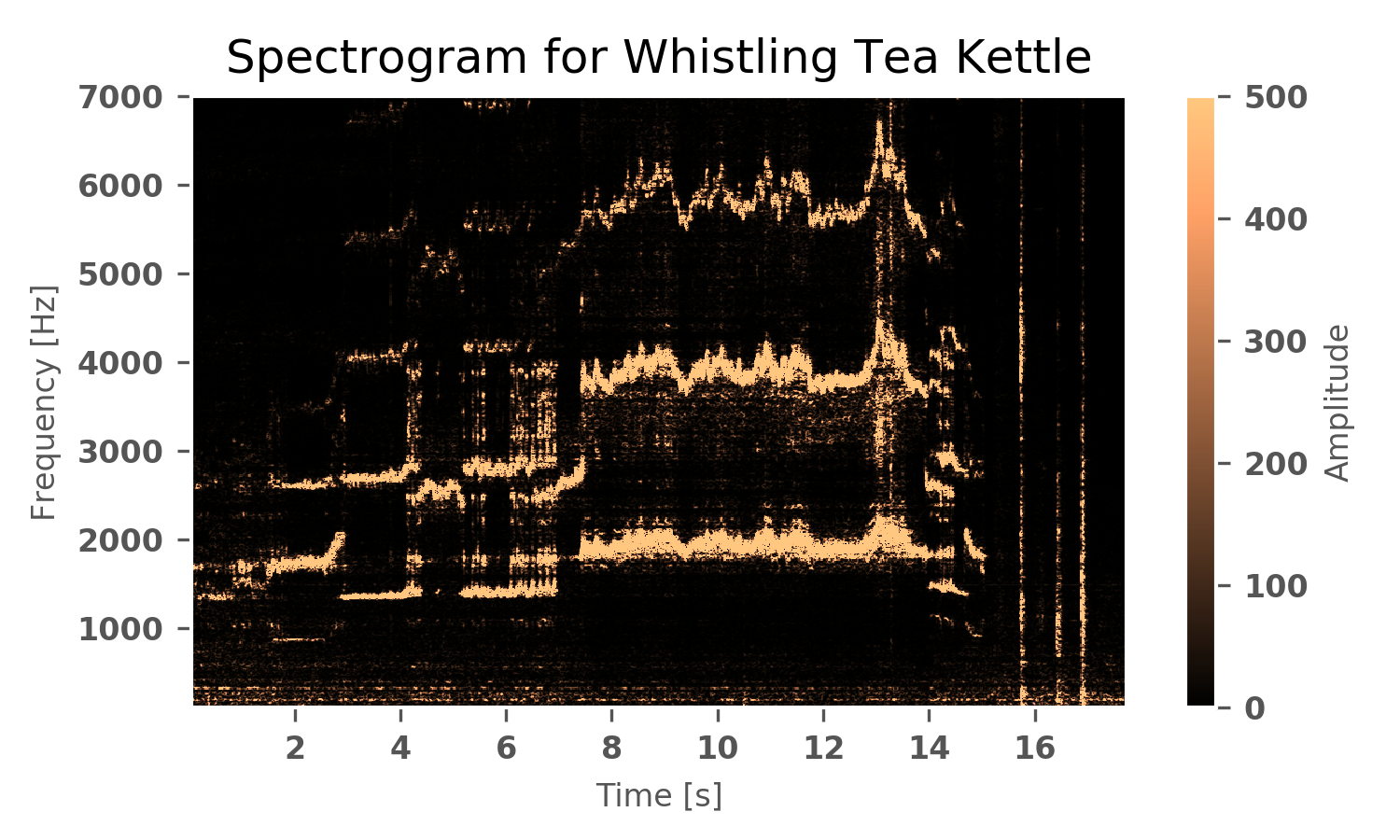
Below is a recording that I made of the tea kettle in my apartment (apologies for the low-quality video). Beneath the video is the real-time spectrogram (frequency vs time plot) that show the frequency behavior of the kettle as it begins to heat up and ultimately reach its peak whistle. After several iterations of heating the kettle, the behavior seen in the video and spectrogram is consistent and repeatable. The characteristic behavior of the kettle is as follows:
kettle starts to heat up - no loud acoustic emission
singular loud tone is emitted and its frequency begins gradually increasing
tone hits a discontinuity and begins emitting loud harmonics
loud harmonics cut in and out and occasionally fluctuate frequency
Spectrogram of a whistling tea kettle. The dominant frequency starts around 1500Hz and continues to climb toward 3000Hz. Several harmonics are present as well, however, they are not open-tube harmonics, which indicates that the theory proposed was incorrect or invalidly applied. While the beginning Helmholtz approximations were somewhat correct and in the correct range, once the steady-state was reached, the theory involving the neck standing waves broke down. It is possible that two mechanisms are at work, such as a fundamental at 2kHz and its open-tube resonance exists at 6kHz, while a second mechanism (such as the Helmholtz tone) is dominant at the 3kHz range. This could be one explanation for the breakdown of the two suggested theories.
At this point, it is not easy to draw distinct conclusions. The problem is that there are too many unknowns and too little information about the system. Perhaps if other variables were known, such as temperature, pressure, or more accurate measurements of the kettle whistle, the problem would be more manageable and better deductions could be made. Unfortunately, the breadth of the simplifications that were made and the culmination of inaccurate assumptions and error-prone approximations result in the inability to truly close this problem.
That being said, it is possible that there are multiple mechanisms at work here. One theory is that the Helmholtz frequency was dominating during the ramp-up to full whistle (the large slope in the spectrogram), and the fully-established realm is both the Helmholtz frequency and the neck standing wave resonances. If this is true, it would mean that during the steady-state period the dominant frequency would be 3kHz and a Helmholtz resonance, while the lower 2kHz and its harmonic at 6kHz are neck standing wave resonances. This must be true because if the system behaves as originally expected, there needs to be resonances an odd multiple apart (remember the 2n-1 in the open-ended channel equation).
Regrettably, it appears that in other runs of the experiment the dominant frequencies are all increasing multiples of each other (not exclusively odd multiples as is the case for closed-ended tubes) indicating that the open-ended pipe assumption could not be true. I think there is definitely a series of mechanisms at work to produce these discontinuities that we see in the profiles, and it also appears that these frequencies along with the discontinuities and profiles can all be described roughly using the Helmholtz approach as well as the neck length to approximate standing wave resonances. In that regard, I would say this experiment was more of an exploration of dimensional analysis and its application to real-world problems. It is with great disappoint that I have to leave this experiments as it is, but it has progressed outside the scope of this blog.
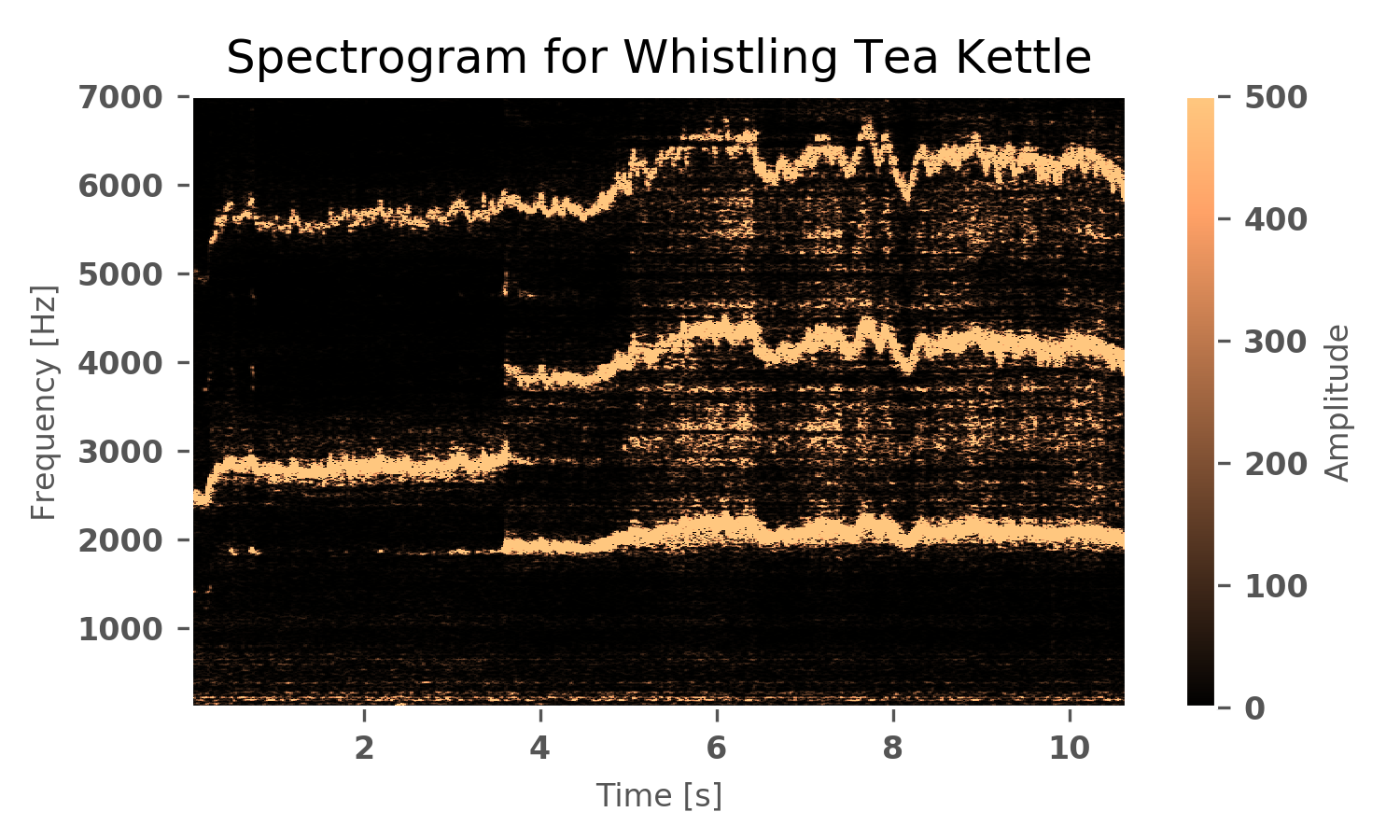
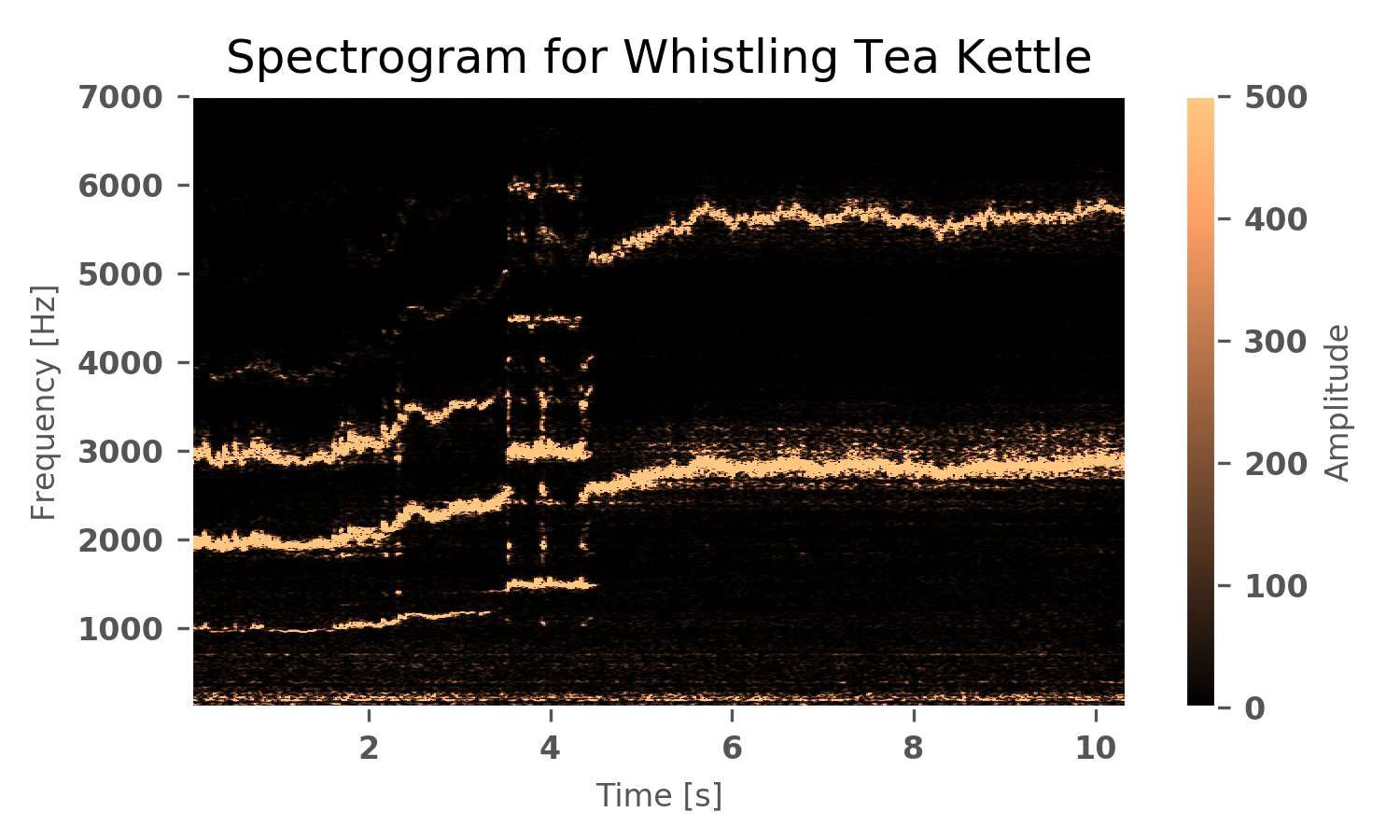
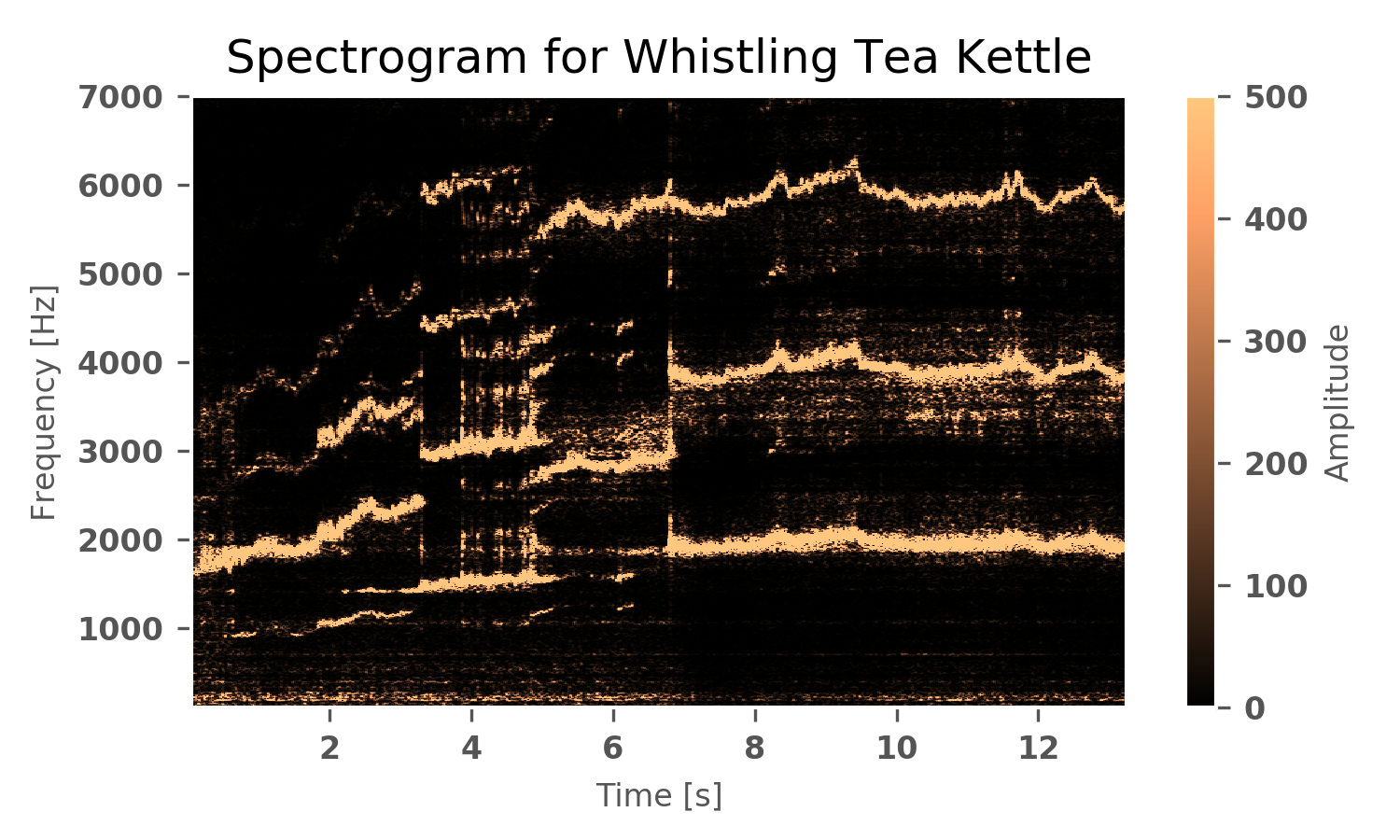
Gallery showing 5 other tea kettle experiments, all of which have similar results that include a transient period during heatup, a sporadic period after some time, and then a pseudo-steady state period that occasionally oscillates around its central frequency. There are also consistent harmonics that do not follow the open-ended channel odd incremental increase - indicating that there is another dominant mechanism producing harmonics than originally thought.
Hypotheses and Conclusion
There are countless questions and not enough answers to accompany this complex problem. After investigating the standing wave phenomena and the application of Helmholtz resonators I was sure they would apply nicely to this problem of a steam kettle. Much to my dismay, I am not able to give much insight into the comparison between the theory and experiments carried out here. I attempted to find the mechanisms that produce the sound that so uniquely represents a tea kettle, and I was met with befuddlement. There appears to be a strong correlation between the length of the neck and the fundamental frequency of the system.
A positive conclusion can be drawn from the approximations of both the neck standing waves and the Helmholtz resonance approximation: both seemed to give fundamental frequencies right around the range of the actual observed fundamental frequency. This could also signify that a positive feedback mechanism could be causing harmonics to form in the whistle, creating the observed incremental harmonics, however, this is only speculation. Overall, the experiments demonstrated the complex nature of a boiling kettle. The problem is incredibly difficult due to the highly complex setup. There is a constant increase in temperature until it reaches the steady-state, there are multiple states that produce discontinuities in sonic behavior, and there are even sudden changes during the perceived steady-state periods that causes jumps in frequency. All of these inconsistencies and inhomogeneities in temperature and pressure result in only a partially understood system. Perhaps I will return and make further developments on this complex topic, but for now - it will have to remain a problem unsolved.
See more in Engineering: